�����x���A�D��֧һ����Ƹ��ԇ�W(w��ng)�A�D�����l(f��)����2021����֧һ���Мy�俼������(sh��)��ֵ���}��ο������������Ԕ����ϢՈ��x����!�����YӍՈ�Pע�A�D��֧һ����ԇ�Ź���̖(htszyf)�����gӭ����ȫ����֧һ���俼����Ⱥ��764172889���
��������(sh��)��ֵ���}�mȻ���ǟ��T�}�ͣ���������Ҳ�������Q��ʽ�M�п�����������@��}Ŀ���շ��������÷֣��������ˆ�?���쎧�I��ҌW��һ�¡�
����֪�R�c
����1.�}���R�e�����Խ�(j��ng)���������}����ʽ���F(xi��n)��������ʲô�r��@��������������Ƕ���?
����2.�}�ͣ��o��һ��������Ȼ���M���{(di��o)������������������F(xi��n)“ÿ……��……”�����������L��������……�@�����/����Ƕ���������
�������cʽ��
����1. ����(j��)�l����ʽ���������Ƀɂ���̖��˵���ʽ�������
����2. ���ʹ��ʽ����0�r�������x�ăɂ�ֵ��
����3. Ӌ��ɂ�x��ƽ��ֵ������˕ryȡֵ���������
����4. ������и�����(sh��)��x����ٕr����(sh��)��ȡ�����ֵ�������
����(1)y=(35-5x)(3+x)���������x1=7����x2=-3�������x=(x1+x2)/2=(7-3)/2=2�r����������(sh��)��ȡ�����ֵ��
����(2)y=(18+3x)(28-2x)������x1=-6����x2=14�������x=(x1+x2)/2=(-6+14)/2=4�r�������(sh��)��ȡ�����ֵ���
����(3)y=(150-2x)(100+4x)�������x1=75������x2=-25����x=(x1+x2)/2=(75-25)/2=25�r���������(sh��)��ȡ�����ֵ��
����ʾ��(2020���K)
����ij��Ʒ���M؛�r��80Ԫ��������N�ۆr��100Ԫ�������ÿ����۳�120��������֪�N�ۆrÿ����1Ԫ������ÿ��ɶ��۳�20��������Ҫ���F(xi��n)ԓ��Ʒ���N��������������t�N�ۆr�����͵Ľ��~��
����A.5Ԫ
����B.6Ԫ
����C.7Ԫ
����D.8Ԫ
����������
�����O���rxԪ�Ɍ��F(xi��n)��������������֪“�N�ۆrÿ����1Ԫ��ÿ��ɶ��۳�20��”����{(di��o)�r���N�ۆr��100-xԪ���M؛�r��80Ԫ�����t���r���������(100-x-80)=20-xԪ;���r����N����120+20x���������
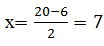
��������(j��) ������=������ × ��(sh��)�� �ɵ��������@�õĿ�����y=(20-x)×(120+20x)�������y=0���t20-x=0��120+20x=0�������x1=20�������x2=-6�����r��������@�ÿ����������������ʑ�ԓ���r7Ԫ����
���������_�𰸞�C�������
|
���擌��֪ |
һ��һ��ԃ |
 |
�Pע�A�D��֧һ����^(q��)��ԇ�W(w��ng) |
 |
���r�˽Ȿ�ؿ��� |
|
���^(q��)���擌�ȿ� |
���M�Iȡ�俼�Y�� |
|
���I(y��)�ͷ��������� |
��ԃ�ϰ��n�� |
������admin��



 �ŵ��
�ŵ��

 �~̖���
�~̖���




 ӛס��
ӛס��
















![�e���]��](http://u2.huatu.com/xuyl/20181015jbyx.png)